Here are some of my thoughts on
Large Numbers MIDDLE KINGDOM -- HOW AND
WHY THINGS HAPPEN
Collected Wisdom on April, 25 1996 By Philip Jackman
The question: "We're all familiar with
the numbers million, billion and trillion," wrote another John
Wright, this one from Scarborough, Ont. "I've even seen reference
to the googol, which is 1 followed by 100 zeros, and the googolplex, which
is 10 times that amount. What is the largest finite number that has a name?"
The answer: Before we go any further, Jim Kendall of Ottawa
wants to make a correction. "Your definition of a googolplex is in
error. It should be 10 raised to the power of a googol--that is, 1 followed
by a googol of zeros. Your definition, 10 times a googol, would be 1 followed
by 101 zeros."
Having got that straight, he informs us that the googol was invented by
Edward Kasner, a U.S. mathematician.
To illustrate the idea of a very large but finite number, Kasner asked
some children in a kindergarten what was the largest number they could
think of. "A child wrote 1 with 100 zeros. Kasner asked his nine-year-old
nephew to name it. The nephew suggested 'googol' after Barney Googol, a
comic-strip character in the 1930s and forties with bulging eyes."
This is where Mike Wingham of Calgary takes up the story.
"At the same time, the nephew proposed the name 'googolplex' for a
much larger number: a 1 followed by 'writing zeros until you got tired.'
Kasner, feeling this definition lacked sufficient mathematical rigour,
redefined a googolplex as a 1 followed by a googol of zeros.
"To get a feel for the size of a googolplex, the number of electrons
in the universe was estimated earlier this century to be a 1 followed by
79 zeros--much less than a googol, let alone a googolplex."
However, our old pal Marc A. Schindler of Spruce Grove, Alta., says
there's an even larger number called a "moser," named after Canadian
mathematician Leo Moser. However, the explanation of its magnitude went
over CW's head by a googol of country miles. Suffice it to say, a googlplex
is just about as big as number as you'll ever need.
Collected Wisdom, which appears each Thursday, can be
reached at wisdom@GlobeAndMail.ca
on the Internet. And visit us each week on the World Wide Web at http://www.TheGlobeAndMail.com/
Copyright © 1996 The Globe and Mail
®
In this essay we shall discuss complex numbers. These are expressions of the form a + ib, where a and b are "real" numbers and i is a symbol for the square root of negative one. Unfortunately, the words "real" and "imaginary" have connotations that somehow place the square root of -1 is a less favorable position than the square root of 2 in our minds. As a matter of fact, a good deal of imagination, in the sense of inventiveness, has been required to construct the real number system, which forms the basis of calculus. In this article we shall review the various stages of this invention. The further invention of a complex number system will then not seem so strange. It is fitting for us to study such a system, since modern engineering has found therein a convenient language for describing vibratory motion, harmonic oscillation, damped vibrations, alternating currents, and other wave phenomena.
The earliest stage of number development was the recognition of the counting numbers 1,2,3,..., which we now call the natural numbers, or the positive integers. Certain simple arithmetic operations can be performed with these numbers without getting outside the system. That is, the system of positive integers is closed with respect to the operations of addition and multiplication. By this we mean that if m and n are any positive integers, then
m + n = p
and
mn = q
are also positive integers. Given the two positive integers on the left-hand side of either equation, we can find the corresponding positive integer on the right. More than this, we may sometimes specify the positive integers m and p and find a positive integer n such that
m + n = p.
For instance, 3 + n = 7 can be solved when the only numbers we know are the positive integers. But the equation 7 + n = 3 cannot be solved unless the number system is enlarged. The number concepts that we denote by zero and the negative integers were invented to solve equations like that. In a civilization that recognizes all the integers
...,-3,-2,-1,0,1,2,3,...,
an educated person may always find the missing integer that solves the equation
m + n = p
when given the other two integers in the equation.
Suppose our educated people also know how to multiply any two integers of the set shown. If, as above, they are given m and q, they discover that sometimes the can find n and sometimes they can't. If their imagination is still is good working order, they may be inspired to invent still more numbers and introduce fractions, which are just ordered pairs m/n of integers m and n. The number zero has special properties that may bother them for a while, but they ultimately discover that it is handy to have all ratios m/n, excluding only those having zero in the denominator. This system, called the set of rational numbers, is now rich enough for them to perform the so-called rational operations of arithmetic:
on any two numbers in the system, except that they cannot divide by zero.
The geometry of the unit square and the Pythagorean Theorem showed that
they could construct a geometric line segment which, in terms of some basic
unit of length, has a length equal to the square root of 2 [2(½)].
Thus they could solve the equation x² = 2 by a geometric construction.
But then they discovered that the line segment representing 2 
(2) and
the line segment representing the unit of length 1 were incommensurable
quantities. This means that the ratio (2 (2))/1 cannot be expressed
as the ratio of two integral multiples of some other, presumable more fundamental,
unit of length. That is, our educated people could not find a rational
number solution of the equation x² = 2.
There is a nice algebraic argument that there is no rational number whose square is 2. Suppose that there were such a rational number. Then we could find integers p and q with no common factor other that 1, and such that
p² = 2q².
Since p and q are integers, p must then be even, say
p = 2P
where P is an integer. This leads to
2P² = q²,
which says that q must also be even, say
q = 2Q,
where Q is an integer. But this is contrary to our choice of p and q as integers having no common factor other that 1. Hence there is no rational number whose square is 2.
Our educated people could, however, get a sequence of rational numbers 1/1, 7/5, 41/29, 239/169, ..., whose squares form a sequence 1/1, 49/25, 1681/841, 57,121/28,561, ..., that converge to 2 as its limit. This time their imagination suggested that the needed the concept of a limit of a sequence of rational numbers. If we accept the fact that an increasing sequence that is bounded from above always approaches a limit, and observe that the sequence shown has these properties, then we want it to have a limit L. This would also mean, from looking at the sequence of the squares, that L2 = 2, and hence L is not one of our rational numbers. If to the rational numbers we further add the limits of all bounded increasing sequences of rational numbers, we arrive at the system of all "real" numbers. The word real is placed in quotes because there is nothing that is either "more real" or "less real" about this system than there is about any other well-defined mathematical system.
Imagination was called upon at many stages during the development of the real number system from the system of positive integers. In fact, the are of invention was needed at least three times in constructing the systems we have discussed so far:
These invented systems form a hierarchy in which each system contains the previous system. Each system is also richer than its predecessor in that it permits additional operations to be performed without going outside the system. Expressed in algebraic terms, we may say that
Every student of algebra is familiar with the formula that gives the solutions of this last type of equation, namely,
x = [-b +- (b² -4ac)(½)]/2a
and familiar further with the fact that when the discriminant, d = (b² - 4ac) is negative, the solutions of the formula do not belong to any of the systems discussed above. In fact, the very simple quadratic equation
x² + 1 = 0
is impossible to solve if the only number systems that can be used are the three invented systems mentioned so far.
Thus we come to the fourth invented number system, the set of all complex
numbers a + ib. We could, in fact, dispense entirely
with the symbol i and use a notation like (a,b). We
would then speak simply of a pair of real numbers a and b.
Since, under algebraic operations, the numbers a and b are
treated somewhat differently, it is essential to keep the order straight.
We therefore might say that the complex number system consists of the set
of all ordered pairs of real numbers (a,b), together with
the rules by which they are to be equated, added, multiplied, and so on,
listed below. We shall use both the (a,b) notation and the
notation a + ib. We call the a the "real part"
and b the "imaginary part" of (a,b). We
make the following definitions.
The set of all complex numbers (a,b) in which the second number is zero has all the properties of the set of ordinary "real" numbers a. For example, addition and multiplication of (a,0) and (c,0) give: (a,0) + (c,0) = (a + c,0) and (a,0) * (c,0) = (ac,0), which are numbers of the same type with the "imaginary part" equal to zero. In particular, the complex number (0,0) plays the role of zero in the complex number system and the complex number (1,0) plays the role of unity.
The number pair (0,1), which has the "real part" equal to zero and the "imaginary part" equal to one has the property that its square,
(0,1) * (0,1) = (-1,0)
has the "real part" equal to minus one and "imaginary part" equal to zero. Therefore, in the system of complex numbers (a,b) there is a number x = (0,1) whose square can be added to unity = (1,0) to produce zero = (0,0); that is,
(0,1)² + (1,0) = (0,0).
The equation x² + 1 = 0 therefore has a solution x = (0,1) in this new number system.
You are probably more familiar with the a + ib notation than you are with the notation (a,b). And since the laws of algebra enable us to write (a,b) = a(1,0) + b(0,1) while (1,0) behaves like unity and (0,1) behaves like the square root of minus one, we need not hesitate to write a + ib in place of (a,b). The i associated with the b is like a tracer element that tags the "imaginary part" of a + ib. We can pass at will from the realm of ordered pairs (a,b) to the realm of expressions a + ib, and conversely. But there is nothing less "real" about the symbol (0,1) = i than there is about the symbol (1,0) = 1, once we have learned the laws of algebra in the complex number system. To reduce any rational combination of complex numbers to a single complex number, we need only to apply the laws of elementary algebra, replacing i² wherever it appears by -1. [...]
THE FUNDAMENTAL THEOREM OF ALGEBRA
One may well say that the invention of (-1)(½) is all well and good and leads to a number system that is richer than the real number system alone; but where will this process end? Are we also going to invent still more number systems so as to obtain (-1)(¼), (-1)(1/6), and so on? By now it should be clear that this is not necessary. These numbers are already expressible in terms of the complex number system a+ ib. In fact, the Fundamental Theorem of Algebra says that with the introduction of complex numbes we now have enough numbers to factor every polynomial into a product of linear factors and hence enough numbers to solve every possible polynomial equation.
The Fundamental Theorem of Algebra Every polynomial of the form
a0zn + a1z(n-1) + a2z(n-2) + ... + a[n-1]z + a[n] = 0,
in which the coefficients a0, a1, ..., a[n]
are any complex numbers, whose degree n is greater than or equal
to one, and whose leading coefficient a0 is not zero, has exactly
n roots (given that each occurrence of a multiple root is counted
as a distinct root).
The theorem is stated here without proof, but it is helpful to note the following sequence of complex numbers.
The list is now complete. Since the powers of i are modulus four, any power of i greater than this may have it's exponenet reduced by multiples of four, as this merely represents dividing by one.
TAYLOR'S SERIES AND THE EULER RELATIONSHIP
Taylor's Series (named after the English mathematician Brook Taylor, 1685-1731) are defined for a function x on an interval about a, that the function is equal to the function evaluated at a, plus the first derivative of the function evaluated at a times (x-a), plus the second derivative of the function evaluated at a divided by two factorial times (x-a) squared, plus and so on through the nth derivative evaluated at a divided by n factorial times (x-a) to the nth power. The remainder (beginning with the (n-1)st term) is such that the total error introduced by truncating the infinite series will be smaller than the (n-1)st term:
f = f(a) + f'(a)(x - a) + f"(a)/2!(x - a)² + ... + f(n)(a)/n!(x - a)n + R(x,a),
where the remainder R(x,a) = f(n+1)(c/(n+1); a < c < x.
Taylor series are useful to calculate the values of irrational functions to as many decimal place accuracy as desired. It can be shown that:
ex = 1 + x + x²/2! + ... + xn/n! +...
sin x = x - x3/3! + x5/5! - + ...
cos x = 1 - x²/2! + x4/4! - + ...
Consider for a moment the value of e(ix) (e raised to the ix power). By substituting "ix" for "x" in the Taylor Series expansion and collecting terms, we find that the real terms constitute the Taylor Series for cos x and the imaginary terms constitute the Taylor Series for sin x. That is, e(ix) = cos x + i sin x. (This is known as Euler's formula for the mathematician Leonhard Euler, 1707-1783.)
Now let x = pi:
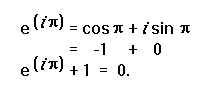Reflecting
on this remarkable statement for a moment, we see in one simple step we
have included both e and pi, the two most well-know irrational
numbers; i, the imaginary square root of minus one; plus, the fundamental
of the four basic arithmetic operations (since multiplication is repetitious
adding and subtraction and division are the reverse processes of addition
and multiplication); one, the identity number of multiplication and the
most elementary counting number; zero, the identity number of addition
and the first imaginative creation of defined number systems, and the equal
sign, the most fundamental concept in all of mathematics.
The four formulae collectively known as Maxwell's Equations define the realm of electromagnetic energy, which includes all radio waves, light, and is the basis for most of our modern technological society.
Here are the four equations, both symbolically and in text. Below there is a brief discussion of how Maxwell used these four equations in concert to
Gauss' Law
The divergence of the electric flux density (the sum of the electric flux density through a closed surface) is equal to the total charge density contained therein. (Electric flux lines emanate from positive charges [sources] and converge on negative charges [sinks].)
Faraday's Law
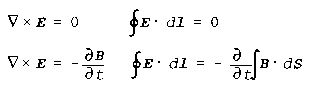
The curl of the electric field (the total product of the electric field
and current over any closed path) is zero (time invariant case) or equals
the time rate of change in the magnetic flux density. (An electrostatic
field is conservative of energy; a time-varying electric field gains its
energy from or loses it to a concurrently time-varying magnetic field.)
Ampere's Law
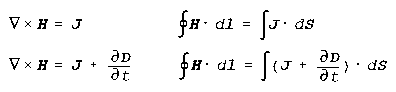
The curl of the magnetic field (the total product of the magnetic field
and current over any closed path) equals the volume current density (time
invariant case) or the volume current density and the time rate of change
of the electric flux density. (A changing magnetic field results from electrical
current, or from the sum of the current and a changing electric field.)
Gauss' Law for magnetic fields
The divergence of the magnetic flux density (the sum of the magnetic flux
density over any closed path) is zero. (Magnetic fields have no poles
[sources or sinks]; magnetic lines of flux do not terminate.)
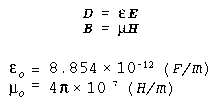
The electric flux density is proportional to the electric field by the
permittivity of the medium; the magnetic flux density is proportional to
the magnetic field by the permeability of the medium. The permittivity
and permeability of free space are based on experimental observations.
A general wave function y(x,t) is a solution of a differential equation called the wave equation. The wave equation relates the second partial derivative with respect to x to the second derivative with respect to t. We can obtain the wave equation by recalling that the function
y(x,t) = y' sin(kx-
t)
is a particular solution for harmonic waves. It is useful to write the
angular frequency in terms of the velocity v and a wave
number k; that is, = kv. Then the harmonic wave
function is
y(x,t) = y' sin(kx-kvt).
The derivative with respect to x, holding t constant, is
y/dx = k y' cos(kx-kvt).
The second derivative with respect to x is
The second derivative with respect to t, holding x constant, is
Combining these two gives us
[ [
[
[
Now, in free space (no charges or currents are present) using Gauss' Law
div D =
[v]
(and for magnetics)
div B = 0
we see that, since [v] = 0, net electric or magnetic flux through any closed surface is zero.
In rectangular coordinates, with an electric field propagating in the +x direction, the net flux through each face of a cube is considered. The flux entering or leaving the cube on the two faces parallel to the constant y or the two parallel to the constant z planes is zero since they are orthongal to the E field. Also, since there are no charges, the net flux over the closed surface of the cube must be zero (it contains no charges), therefore the field is constant in the +x direction, and does not contribute to any electromagnetic waves. By a similar reasoning, if the B field propagates in the +y direction, then B must also be constant in the +y direction. Thus, any variation in either field must be perpendicular to both fields.
We now employ Maxwell's other two equations to relate the time and spatial derivatives of the two fields. From before, with E in the +x direction, we can tie the time dependence of By to the spatial dependence of Ex by applying Faraday's Law around the closed path 
x-z in the xz-plane.
(E·dl) = -
(B·dS)]
The line integral is taken around a differential element in the xz-plane and
Since Ex is constant in the +z direction, the two terms containing
z are zero. So,
= Ex(z2)
- = [Ex(z2) - Ex(z1)]
- =
As z becomes very small, Ex goes to (Ex/z) xz and
Through the same area, the magnetic flux is
So,
(
(
Any variance of Ex over the z direction is equal in magnitude to a variance of By over time.
We can manipulate Ampere's Law
using D = 
E
and B = µH and recalling that we are operating in free
space. This means there is no current (J = 0) and
= 0, µ = µ0.
By a process similar to the above,
(
Any variance of By over the z direction is equal in magnitude
to a variance of Ex over time by a proportional constant of µ00.
Now if we take the two equations
( (
we can eliminate either Ex or By by differentiating both equations with respect to z or t. For instance, let us differentiate the equation on the left with respect to z:
(
(
(we switch the order of differentiation) and now substitute
(
into
(
(
(
We now have
(
If we had chosen to differentiate with respect to t instead we would have been led to
(
We can see that these are in the form of the wave equation, where the proportionality factor is the inverse of the velocity of the wave squared. That is,
µ0
leads to
v = 1/
To verify this, let us put in the observed values and manipulate both the quantities and units.
µ0 = 4 × 10-7
[H/m] [F/m] µ0 [H F/m²] [F = C/V, V = J/C leads to F = C²/J] [H = J/A², A = C/s leads to H = Js²/C²] µ0 [Js²C²/C²m²J] µ0 [s²/m²] [s/m] 1/ [m/s],
which equals c, the speed of light. 
Thus, Maxwell not only postulated the existence of electromagnetic waves before they had been observed or could be demonstrated, but he correctly predicted that they traveled orthogonally to both the E and B fields which produced them, and that they traveled at the speed of light.
Shown at left is an overview of the entire electromagnetic spectrum, "DC to light." The regions which have been given common names (such as radio bands, UHF, VHF; radar bands, G-band, Ku-band; or colors of light) are identified.
denotes the Greek letter delta. denotes the Greek letter epsilon. denotes the Greek letter pi. denotes the Greek letter rho. denotes the Greek letter omega. . ( ). ( ) and ( ). Thus, 1/(µ00) denotes "1 divided by the square root of mu-sub-0 times epsilon-sub-0" where the last two characters are the usual representation of free space permeability and permittivity, respectively.